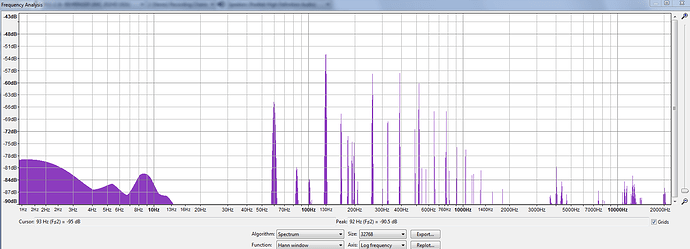
I hope you read and learned something from the first project - Audio Pass Through. Let’s expand on that and make a simple distortion effect. I took the example provided by Daisy and broke it down a bit.
How does distortion work? We’re going to take a look at soft clipping and hard clipping. Here’s a quick breakdown from wikipedia Distortion (music) - Wikipedia
#include <DaisyDuino.h>
DaisyHardware hw;
float hardClip(float in) {
in = in > 1.f ? 1.f : in;
in = in < -1.f ? -1.f : in;
return in;
}
static void AudioCallback(float *in, float *out, size_t size)
{
float Gain = 100;
for(size_t i = 0; i < size; i+= 2)
{
float wet = in[i];
wet *= Gain;
wet = hardClip(wet);
out[i] = wet / 6.f;
}
}
void setup() {
hw = DAISY.init(DAISY_PETAL, AUDIO_SR_48K);
DAISY.begin(AudioCallback);
}
void loop() {
// put your main code here, to run repeatedly:
}Our ‘boiler-plate’ stuff is the same so lets take a look at the new stuff starting in the AudioCallback function.
float Gain = 100;All we’re doing here is defining a float variable called ‘Gain’ with a value of 100. It was an arbitrary number I picked that sounded good, you can change that number to see how it affects the signal.
float wet = in[i];Now we’re defining a float variable ‘wet’ as what’s coming in on the input signal. We’ll talk about wet and dry signals in the next project. You may ask, why are we using all of these float variables instead of int? Int’s are only whole numbers, 1, 2, 3, 4, etc. Floats give us decimal places. The converted analog to digital input signal is a level between -1 and 1 so we need to use a float to be able to get decent audio.
wet *= Gain;Here we’re just multiplying the signal by our Gain variable, which we set to 100. This would be the same statement as ‘wet = wet * Gain;’
wet = hardClip(wet);Now we’re going to send the wet variable to the hardClip function to process. For this example, we could just do the distortion processing in the AudioCallback function, but we should get used to using and calling functions.
float hardClip(float in) {
in = in > 1.f ? 1.f : in;
in = in < -1.f ? -1.f : in;
return in;
}In this function, we’re going to take that ‘wet’ variable and now assign it to a float called ‘in’. Keep in mind that because this is a different function than AudioCallback, ‘in’ is an isolated variable and not the same as the ‘in’ in the AudioCallback function. Variables are only used in the function they’re defined in.
The next two lines are comparison operators. It’s basically saying “Is ‘in’ greater than 1? Yes, then in = 1. No then in = in.” It repeats it for the negative portion of the audio signal. This will ensure that the highest and lowest possible values are 1 and -1 (Seeds max and min values), effectively clipping off the signal that goes higher than that. The .f after 1 treats the statement as a float, not sure if it’s needed but it’s a good habit to get into.
Next, we’re going to return the value stored in ‘in’ back to the variable ‘wet’ when we called it from the AudioCallback function.
out[i] = wet / 6.f;Our final piece of code outputs our ‘wet’ signal and divides it by 6. Why are we dividing it by 6? Well, the signal is now amplified above the point that the Seed can handle so it cuts it off at the max. In the last lesson I had mentioned that the guitar signal is much lower than what the Seed normally handles. So now our distorted guitar signal will be MUCH louder than the input. I divided it by 6 just to turn the volume down a bit. Feel free to play with that number to your liking.
So we talked about hard clipping, what about soft clipping?
Let’s replace our hardClip function with a softClip one (or just add a new function)
float softClip(float in) {
if (in > 0)
return 1 - expf(-in);
return -1 + expf(in);
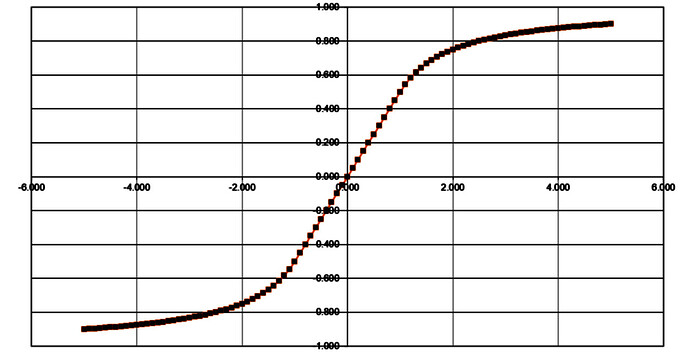
}Now what’s going on here? This statement is saying “if the input signal is greater than 0, then send back ‘1 - expf(-in)’. Otherwise, send back ‘-1 + expf(in)’”. Let’s take it a step further and see exactly what this is doing and how to calculate it. Remember, the Daisy outputs a signal between -1 and 1, we can never have a higher number. Let’s say the input audio level at that sample happened to be a value of 0.1. Let’s plug that into this formula on a calculator: 1 - e^(-0.1) and we should get .095. Now plug in a 1 - e^(-.999) and we should get a .63, which is the highest value we can get. If you plug in and graph out a bunch of different points, it should look like a squished down hard clipped signal like the picture in the wikipedia article. It will effectively reduce the sharp edges of the distortion.
Make sure we change the function we call to
wet = softClip(wet);Compile all that and let’s see what we get. There’s some sweet sounding soft distortion. If you reduce the Gain variable, you may be able to better hear the difference between the hard and the soft clipping.
Hope all of this made some sense. Next up, let’s make a useful effect by digging into the DaisyDuino modules and create some reverb.