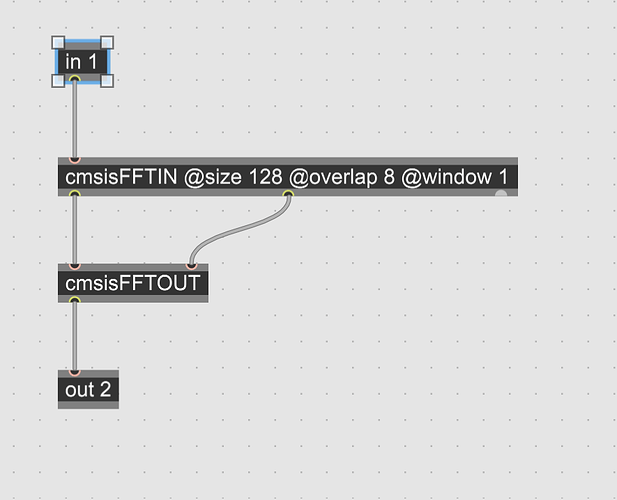
I’m developing an STFT processor for the Daisy with CMSIS Real FFT functions.(using the pfft~ object as an example). I’ll be parsing the exported code, replacing the cmsisFFTIN function with the actual fft routine, and shuffling the signal processing routine around to take care of singe sample/block processing. I have a semi working STFT processor, the issue is with an increase in overlap, the gain increases. I believe I need to normalize the signal.(due to the additions in the overlap process?) I’ve read about peak and rms normalization, but still am unsure on how to best normalize a real time signal. Thank you!
void processBlock(float32_t *pSrc, float32_t *pDst)
{
// incoming signal
for (auto i = 0; i < BLOCK_SIZE; i++)
{
currBlock[i] = *(pSrc++);
}
// join previous and current blocks
arm_copy_f32(prevBlock, &twoBlocks[0], BLOCK_SIZE);
arm_copy_f32(currBlock, &twoBlocks[BLOCK_SIZE], BLOCK_SIZE);
// copy currBlock to prevBlock
arm_copy_f32(currBlock, prevBlock, BLOCK_SIZE);
arm_fill_f32(0.0, outputBuffer, 2 * BLOCK_SIZE - (BLOCK_SIZE / OVERLAP));
for (auto i = 0; i < OVERLAP; i++)
{
float32_t tmp[BLOCK_SIZE];
float32_t res[BLOCK_SIZE];
float32_t cmplxOut[BLOCK_SIZE];
arm_copy_f32(&twoBlocks[i * HOP], tmp, BLOCK_SIZE);
// win_hanning
arm_mult_f32(tmp, window, tmp, BLOCK_SIZE);
// fft
arm_rfft_fast_f32(&S, tmp, cmplxOut, 0);
// process
// ifft
arm_rfft_fast_f32(&S, cmplxOut, res, 1);
// win_hanning
arm_mult_f32(res, window, res, BLOCK_SIZE);
// add to output buffer
arm_add_f32(res, &outputBuffer[i * HOP], &outputBuffer[i * HOP], BLOCK_SIZE);
}
// add previous overlap
arm_add_f32(olap, outputBuffer, outputBuffer, OB_LEN - BLOCK_SIZE);
// store new ovelrap
arm_copy_f32(&outputBuffer[BLOCK_SIZE], olap, OB_LEN - BLOCK_SIZE);
// output BLOCK_SIZE samples
memcpy(pDst, outputBuffer, sizeof(float32_t *) * BLOCK_SIZE);
}